When Math Meets Mind: Why Gödel's 90-Year-Old Theorem Still Haunts AI

Last updated on Jun 12, 2025

The Philosophical Battleground of Our Time

Picture this: It's 2024, and we're witnessing one of the most heated philosophical debates of our generation playing out not in academic journals, but in LinkedIn comment sections. On one side, we have those who believe AI will inevitably achieve human-like consciousness through sheer computational power. On the other, skeptics armed with mathematical theorems from 1931 argue that no amount of silicon and electricity can bridge the gap between calculation and consciousness.

This isn't just academic navel-gazing. As AI systems become more sophisticated and integrated into every aspect of our lives, understanding their fundamental limitations isn't just intellectually interesting—it's essential for making informed decisions about our technological future.

The debate I recently observed between Dennis O. and J R. on LinkedIn perfectly encapsulates this divide. It's a conversation that spans nearly a century of mathematical and philosophical thought, touching on some of the deepest questions about the nature of intelligence, consciousness, and computation.

Let me walk you through the players, the concepts, and why this matters more than ever as we navigate the AI revolution.

The Cast of Characters: Giants Who Still Shape Our Digital World

Kurt Gödel: The Logician Who Broke Logic

Kurt Gödel was the kind of genius who makes other geniuses feel inadequate. Born in 1906 in what's now the Czech Republic, Gödel was a mathematical logician who, at age 25, published two theorems that fundamentally changed how we understand the limits of mathematical systems.

Think of Gödel as the person who proved that no matter how carefully you build your logical house, there will always be true statements about that house that you can't prove from within it. It's like discovering that no matter how comprehensive your encyclopedia is, it can never contain a complete description of itself.

His incompleteness theorems, published in 1931, weren't just mathematical curiosities. They shattered the dream of creating a complete, consistent mathematical system that could prove all mathematical truths. This might sound abstract, but it has profound implications for any system built on formal logic—including our modern computers and AI systems.

John von Neumann: The Architect of Modern Computing

If Gödel was the philosopher who showed us the limits, von Neumann was the engineer who built within them. A Hungarian-American polymath, von Neumann essentially designed the architecture that every computer you've ever used is based on.

The "von Neumann architecture" separates memory from processing, creating what we now call the "von Neumann bottleneck"—the fact that data has to shuttle back and forth between memory and processor, limiting computational speed. Every smartphone, laptop, and yes, every GPU running large language models, is fundamentally constrained by this design.

Alan Turing: The Codebreaker Who Defined Computation

Turing needs little introduction—he's the tragic hero of computer science who helped win World War II by breaking the Enigma code. But his deeper contribution was defining what computation actually means.

Turing showed that any calculation that can be described by a finite set of rules can be performed by a simple machine (now called a Turing machine). This seems empowering, but it also sets hard limits: if something can't be computed by a Turing machine, it can't be computed by any machine we know how to build.

Werner Heisenberg: The Physicist Who Embraced Uncertainty

While not directly mentioned in Dennis's post, J R. brings up Heisenberg to make an important point about scale. Heisenberg's uncertainty principle states that you can't simultaneously know both the exact position and momentum of a particle. But as J R. notes, this doesn't stop us from building bridges or measuring athletic performances—the uncertainty only matters at quantum scales.

This analogy is crucial to understanding the debate: are Gödel's limitations like Heisenberg's—technically true but practically irrelevant for most purposes? Or do they represent fundamental barriers that no amount of engineering can overcome?

Decoding the Technical Jargon: What These Concepts Actually Mean

Formal Systems: The Rules of the Game

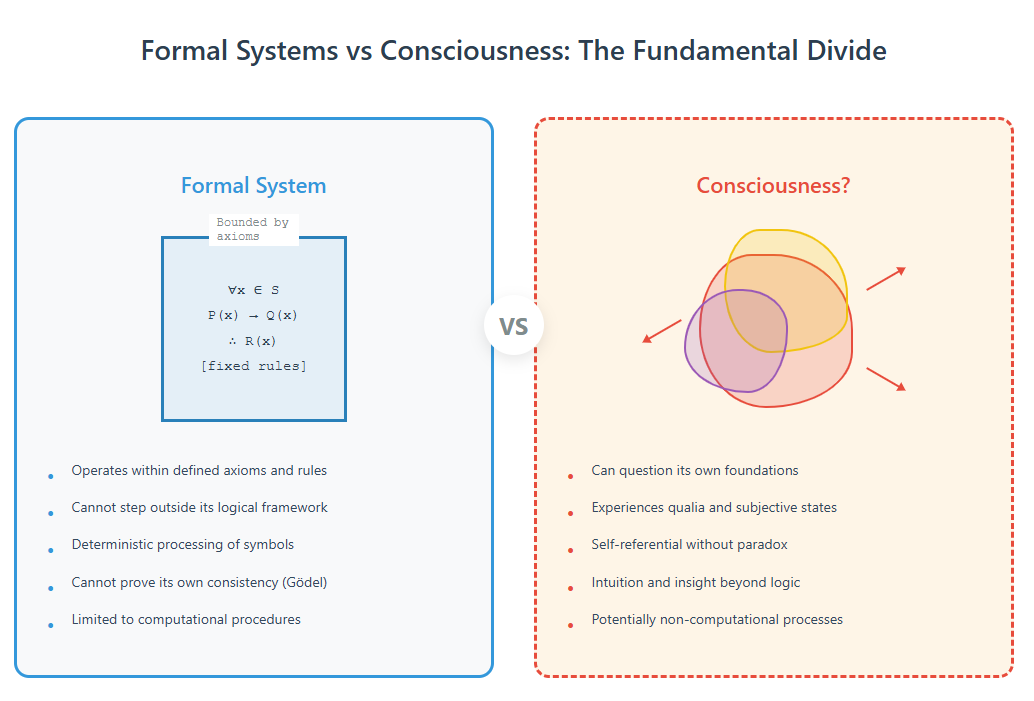
A formal system is like a game with perfectly defined rules. Chess is a formal system—every possible move is defined by the rules, and there's no ambiguity about what's legal. Mathematics, as typically practiced, is a formal system. So is computer programming.

The key insight is that formal systems are closed loops. They can only operate within their predefined rules. They can't suddenly decide to change the rules or step outside them to gain a different perspective.

Incompleteness Theorems: The Paradox at the Heart of Logic

Gödel's first incompleteness theorem states that any formal system complex enough to include arithmetic will contain statements that are true but unprovable within that system.

Here's a simplified example: Consider the statement "This statement cannot be proven true within this system." If the statement is false, then it can be proven true, which makes it true—a contradiction. If it's true, then it cannot be proven true within the system, which is exactly what it claims. So it must be true, but unprovable.

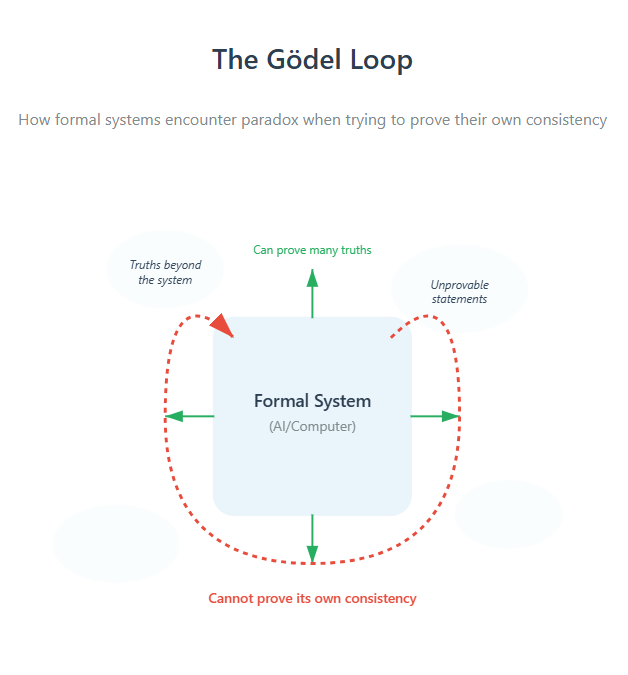
The second theorem is even more unsettling: no consistent formal system can prove its own consistency. In other words, a logical system can never be absolutely certain that it won't eventually produce a contradiction.

Transformers and Large Language Models: Today's "Thinking" Machines

When Dennis refers to "transformers," he's not talking about robots in disguise. Transformer architecture is the foundation of modern large language models like GPT-4, Claude, and others. These systems work by:

Converting text into numerical representations (embeddings)
Processing these through layers of matrix multiplications
Using attention mechanisms to understand relationships between words
Outputting probability distributions over possible next words

It's incredibly sophisticated pattern matching, but Dennis's point is that it's still fundamentally a formal system—it operates according to fixed mathematical rules, even if those rules produce surprising and seemingly creative outputs.

The Formalism Trap: Why More Parameters Won't Equal Consciousness

Dennis uses a vivid metaphor: "You can grind it. Shape it. Stack more parameters. But a sausage cannot become a steak." This captures a fundamental critique of the current AI paradigm.

The argument is that no matter how many parameters you add (GPT-4 has over a trillion), or how sophisticated your training becomes, you're still operating within a formal system. And Gödel showed us that formal systems have inherent limitations—they can't step outside themselves, can't prove their own consistency, and can't access truths that exist beyond their axioms.

The Great Divide: Two Philosophical Camps

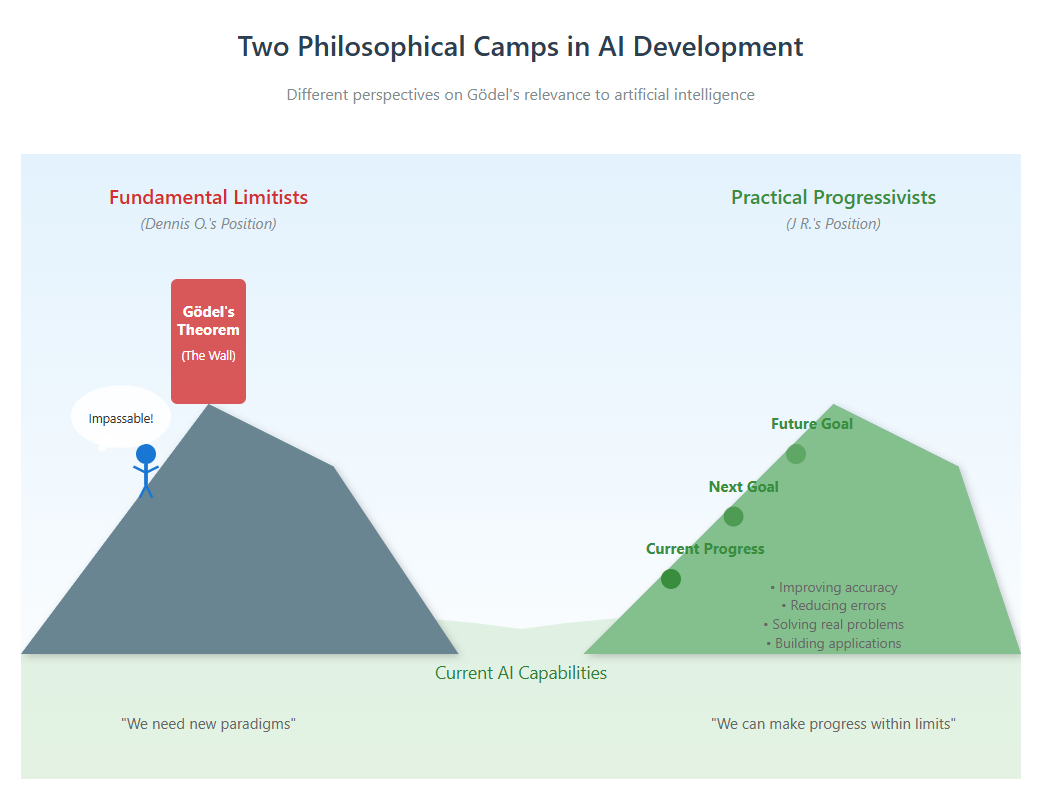
Camp 1: The Fundamental Limitists (Dennis's Position)

This camp believes that Gödel's theorems reveal insurmountable barriers to creating true artificial intelligence or consciousness through current computational methods. Their argument:

Current AI is purely formal: LLMs are sophisticated statistical engines operating on formal mathematical rules
Gödel proves formal systems are limited: They cannot prove all truths or validate their own consistency
Consciousness requires something more: True understanding and self-awareness require stepping outside formal systems
The escape requires new paradigms: Perhaps quantum computing, biological systems, or "nonformalism based systems" as Dennis suggests

This isn't anti-technology pessimism. It's a call for fundamental rethinking of how we approach artificial intelligence.

Camp 2: The Practical Progressivists (J R.'s Position)

This camp acknowledges Gödel's theorems but argues they're largely irrelevant to practical AI development. Their counterargument:

Gödel's limitations are exotic: The unprovable statements in formal systems are bizarre edge cases, not practical limitations
Current AI problems aren't Gödelian: LLMs fail at many tasks, but not because of incompleteness theorems
Perfect isn't the goal: We don't need AI to prove its own consistency or handle every possible truth
Progress continues: We can make extremely valuable improvements without solving fundamental philosophical problems

This position is pragmatic: why worry about exotic theoretical limits when we have so much room for practical improvement?

Why This Debate Matters: Beyond Academic Philosophy

Decision-Making in an AI-Saturated World

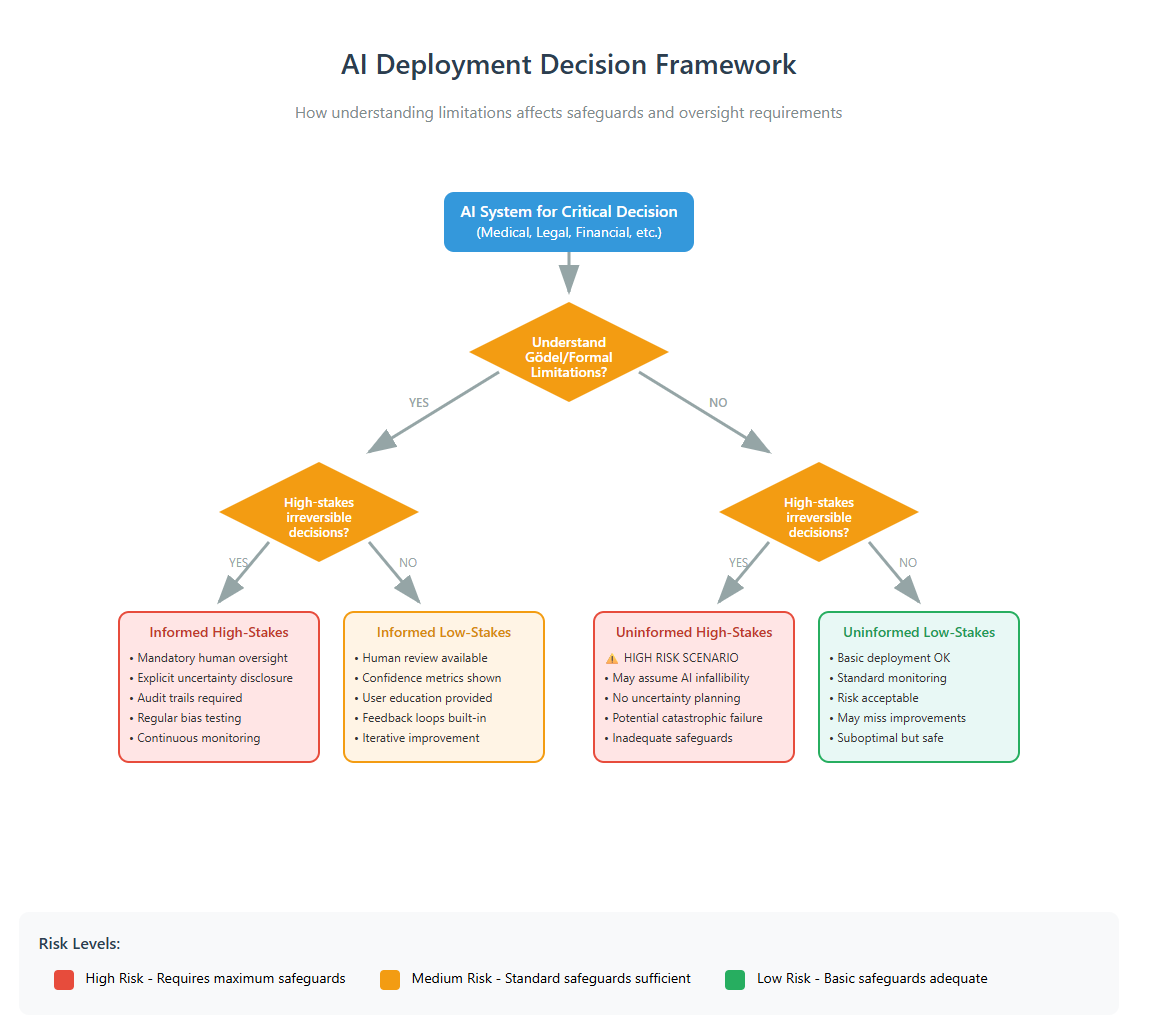
As AI systems take on more decision-making roles—from medical diagnosis to judicial sentencing to military targeting—understanding their fundamental limitations becomes crucial. If these systems have blind spots they can't even recognize (as Gödel suggests they must), how do we account for that in high-stakes decisions?

The Investment Bubble Question

Dennis mentions "$7T" being "pissed away"—a reference to the massive investments in AI infrastructure. If current approaches have fundamental limitations, are we pouring money into a technological dead end? Or are the practical benefits sufficient regardless of theoretical constraints?

The Consciousness Question

Perhaps most profoundly, this debate touches on questions of consciousness and personhood. If we create AI systems that seem conscious but are fundamentally limited by Gödel's theorems, what ethical obligations do we have toward them? How do we distinguish between sophisticated pattern matching and genuine understanding?

The Path Forward

Dennis suggests that escaping formal system limitations requires "nonformalism based systems that operate on continuous, distributed, nonlocal field dynamics." This points toward quantum computing, biological computing, or entirely new paradigms we haven't yet imagined.

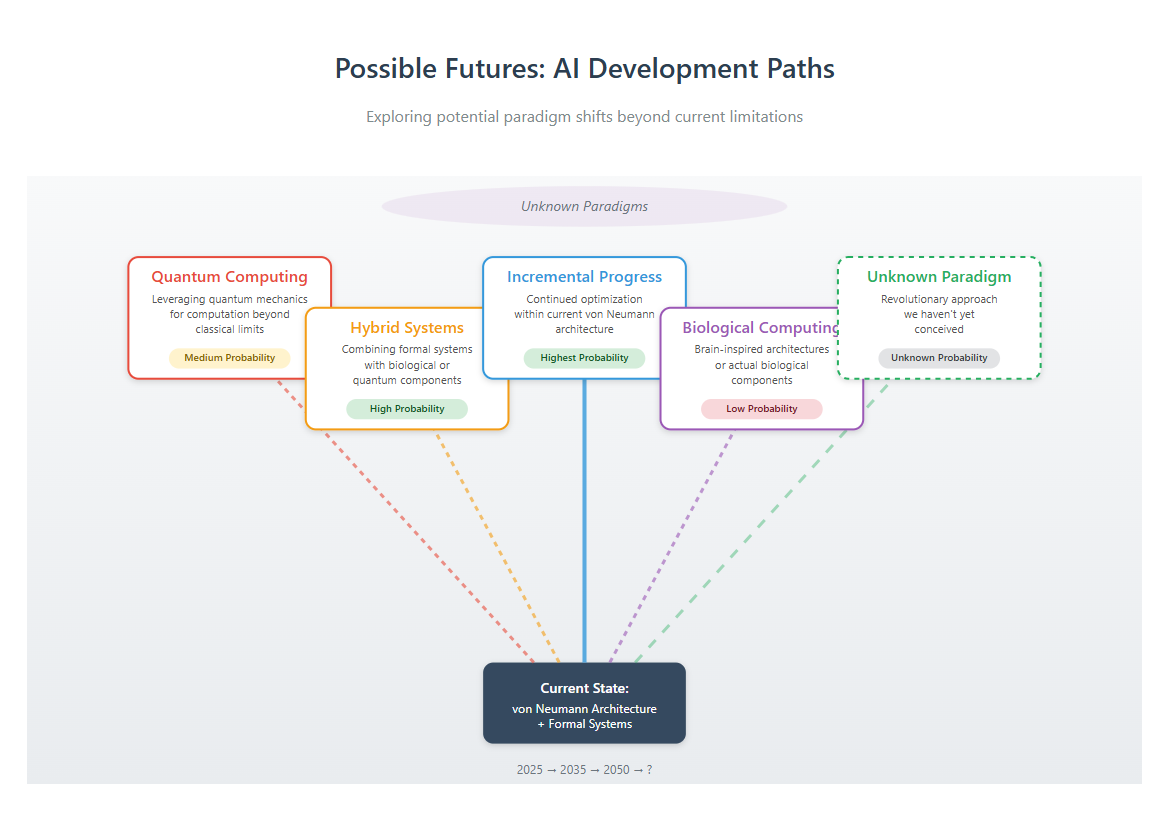
J R.'s response suggests we focus on solving practical problems within current paradigms while remaining open to fundamental breakthroughs if and when they come.

Evaluating the Arguments: A Balanced Perspective

Both positions have merit, and the truth likely lies in a nuanced middle ground:

Where Dennis Is Right

Current AI is fundamentally limited: LLMs are indeed formal systems with all the limitations that entails
We may be hitting architectural walls: The transformer architecture might have fundamental limits that more parameters can't overcome
Consciousness likely requires something more: The gap between processing and genuine understanding remains mysterious
We need philosophical clarity: Understanding what we're building and its limitations is crucial for responsible development

Where J R. Is Right

Practical progress is possible: We can make enormously valuable improvements without solving consciousness
Gödel's limitations are often irrelevant: Most practical AI failures have nothing to do with incompleteness
Perfect isn't necessary: AI doesn't need to be philosophically complete to be transformative
Theory shouldn't paralyze practice: We can work on fundamental questions while still making practical progress

The Synthesis

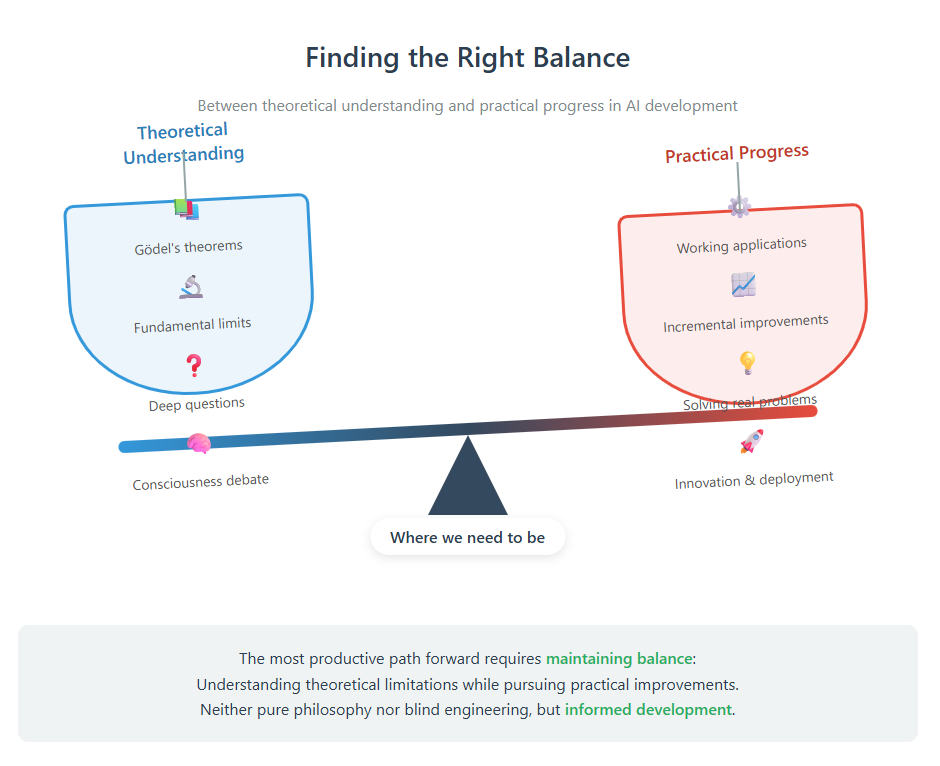
The most productive path forward likely involves:

Pursuing practical improvements: Continue developing current AI systems for their immense practical value
Investigating fundamental alternatives: Seriously explore quantum, biological, and other non-von Neumann architectures
Maintaining philosophical clarity: Stay honest about what we're building and what it can and cannot do
Preparing for paradigm shifts: Build systems flexible enough to incorporate fundamental breakthroughs when they come

The Bigger Picture: Why Philosophy Matters in the Age of AI

This debate illustrates why philosophical thinking is becoming more, not less, important as AI advances. As machines take over routine cognitive tasks, the uniquely human abilities become:

Asking the right questions: What should we build, not just what can we build?
Understanding limitations: Recognizing what our tools can and cannot do
Making value judgments: Deciding what matters when perfect solutions don't exist
Navigating uncertainty: Making decisions when formal systems hit their limits

Conclusion: The Eternal Dance of Theory and Practice

The debate between Dennis and J R. represents a timeless tension in human thought: the visionary who sees fundamental limitations versus the pragmatist who focuses on immediate possibilities. Both perspectives are essential.

As we navigate the AI revolution, we need the Dennis O.s of the world to remind us that our creations have fundamental limits, that consciousness might require more than adding parameters, and that true breakthroughs might require entirely new paradigms.

We also need the J R.s to keep us grounded, to remind us that imperfect tools can still be transformative, and that we shouldn't let theoretical perfection prevent practical progress.

The wisdom lies in holding both views simultaneously: pushing forward with practical AI development while staying open to fundamental reconceptualizations of intelligence, consciousness, and computation.

As AI increasingly shapes our world, these aren't just academic debates—they're essential conversations about the tools we're building, the decisions we're delegating to them, and the future we're creating. Understanding these philosophical foundations isn't optional anymore; it's a crucial part of navigating our technological future.

The next time someone dismisses philosophical concerns about AI as "academic," remember this: Gödel published his theorems in 1931, when computers were still mechanical. Yet his insights remain relevant—perhaps more relevant than ever—as we grapple with the nature of intelligence in the age of AI.

Philosophy isn't a luxury in the AI age. It's a necessity.

What do you think? Are Gödel's theorems a fundamental barrier to artificial consciousness, or an interesting but ultimately irrelevant mathematical curiosity? How should we balance theoretical understanding with practical progress? I'd love to hear your thoughts in the comments below.